2022

FIGURE TAXONOMY

an alphabet of ballroom dance steps

The notation of movements of the body has been a topic actively explored since the 17th century. The project explores the opportunities in representing figures of smooth ballroom dance styles - the waltz, the tango, and the foxtrot, in three dimensions.

CONTEXT

Drawing ++

MIT Media Lab

p5js, Open Frameworks, Grasshopper, Rhinoceros3D, Photoshop, Premiere, Illustrator, 3D Printing

SUPERVISORS

Zach Liberman

SOFTWARE

DANCE NOTATION

a history

In the 1680s Pierre Beauchamp developed a dance notation, the Beauchamp-Feuillet notation, which was used to record Baroque dance styles.

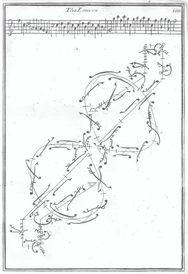
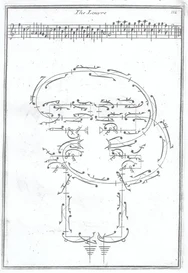
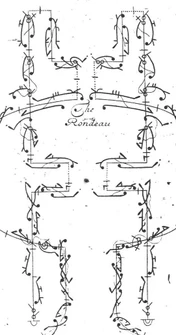
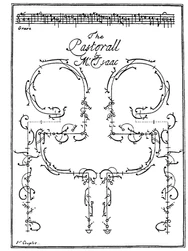
dance-notation-system-page-Choregraphie-examples-de.webp

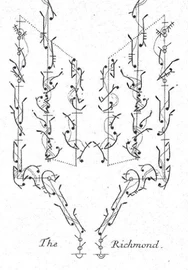
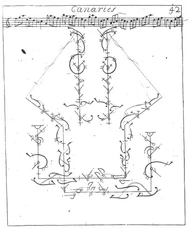
The Smooth dance styles explored in this project are similarly a progressive dances, which means they are directionally moving dances made up of specific collections of steps.

How might one approach drawing ballroom dance in three-dimensions?

DEVELOPING A 3D NOTATION

a process

video isolation of leader and follower

in order to track both, only one can be tracked at a time

let _USE_LIVE_VIDEO = false;

let landmarks;

let W = 640;
let H = 360;

// https://mediapipe.dev/images/mobile/pose_tracking_full_body_landmarks.png
let connects = [0,15,13,11,12,14,16,23,24,25,26,27,28];

function onResults(results) {
if (results.poseLandmarks && results.poseLandmarks.length){
landmarks = results.poseLandmarks;
}
}

let capture;

async function send(){
if (capture.elt.width){
await pose.send({image: capture.elt});
}
setTimeout(send,10);
}

let sel;
let tex=[];
let color = []
let tex_w = 10;

function draw3D() {
noFill();
for (let i =0; i< limbs.length; i++){
Line[i].push([landmarks[limbs[i]].x*W,landmarks[limbs[i]].y*H,landmarks[limbs[i]].z*H]);

texture(tex[i]);
makeMesh(Line[i]);
}
}

}

let trace = [];
let pos = [];
let USE_ORTHO = false;
let limbs = [15,16, 31, 32];
let Line = new Array(limbs.length).fill(0);
for (let i=0; i<limbs.length; ++i) Line[i] = [];

function draw() {
background(220);
translate(-W/2,-H/2);

image(capture,0,0,W,H);

if (landmarks){
// fill(255,255,0);
// noStroke();
// landmarks.forEach(({x,y})=>circle(x*W,y*H,2));

stroke(255);
strokeWeight(2);
noFill();

draw3D();
}
}

function clamp(a,b,c){
return min(max(a,b),c);
}

function keyPressed() {
if (keyCode === ENTER){
for (let i =0; i< limbs.length; i++){
Linev = lineV(Line[i]);
download_file("line"+i+".csv", Linev.map(xyz=>xyz.join(",")).join("\r\n"));
}
}
}

function lineV (LineI)
{
let Linev = [];
for (let i = 1; i < LineI.length; i++){
let p0 = LineI[i-1];
let p1 = LineI[i];
let d = Math.hypot(p0[0]-p1[0],p0[1]-p1[1],p0[2]-p1[2]);
Linev.push([...p0,d]);
}
return Linev;
}

function download_file(pth,text){
var element = document.createElement('a');
element.setAttribute('href', 'data:text/plain;charset=utf-8,' + encodeURIComponent(text));
element.setAttribute('download', pth);
element.style.display = 'none';
document.body.appendChild(element);
element.click();
document.body.removeChild(element);
}

for (let f = 0; f < tot_len; f += spacing){
poly.push(getPointAtLength(f));
}
if(poly.length) poly.push(poly0[poly0.length-1]);
return poly;
}

videos are run through the code

after the video is played, four spreadsheets, one for each limb, are exported

spreadsheets input into grasshopper script to generate geometry

the spreadsheets are parsed and a curve is drawn from the points in the first three columns, the speeds in the fourth column are used as the radii for the pipe